
内容包括数据结构中树的基本概念,实现与应用,以及二叉树,表达式树,二叉查找树,AVL树,伸展树,B+树,以及Java中HashMap的内部实现结构。
数据结构中树的基本概念
树的预备知识
树的递归方式定义:一棵树是一些节点的集合。这些集合可以是空集,若不是空集,则由称作根的节点r以及0个或者多个非空的(子树)T1,T2,….Tk组成,这些子树中每一棵的根都被来自根r的一条有向的边所连接。
一个树是由N个节点和N-1条边的集合。(每条边都将由某个节点连接到它的父亲,而除去根节点外每一个节点都有一个父亲)
没有儿子的节点称为树叶(叶节点),具有相同父亲节点的节点为兄弟。
从节点n1到nk的路径定义为节点n1,n2,…,nk的一个序列,使得对于1<=i长是为该路径上边的条数,即k-1。在一棵树中从根到每个节点恰好存在一条路径。
对任意节点ni,ni的深度为从根到ni的唯一路径的长。ni的高是从ni到一片树叶的最长路径的长。(不同的书定义不一样,知道这个概念就好) 参考《Data Structures and Algorithm Anylysis in Java》
树的实现
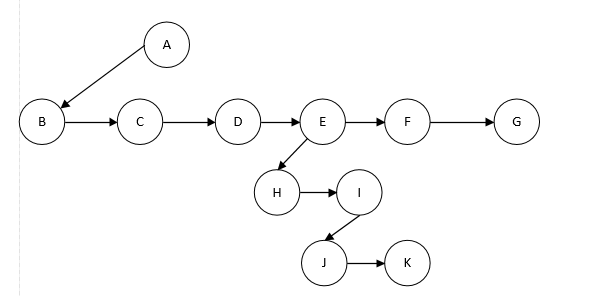
一种简单的实现方式:将每个节点的所有儿子都放在树节点的链表中。
class TreeNode{
Object element;
TreeNode firstChild;
TreeNode nextSibling;
}
其中firstChild(第一个儿子)的链,nextSibling(下一个兄弟)的链。
如上图所示,E有一个链指向第一个儿子(H),也有一个链指向下一个兄弟(F)。
树的应用
先序遍历:访问根节点;访问根节点的左子树;访问根节点的右子树
一个应用就是列出目录中的所有文件的名字:
private void listAll(int depth) {
printName(depth);//Print the name of the object
if (isDirectory())
for each file c in thid directory (for each child)
c.listAll(depth + 1);
}
pulic void listAll() {
listAll(0);
}
后序遍历:访问根节点的左子树;访问根节点的右子树;访问根节点
一个应用就是算出磁盘的大小:
public int size() {
int totalSize = sizeOfThisFile();
if (isDirectory())
for each file c in thid directory (for each child)
totalSize += c.size();
return totalSize;
}
中序遍历:访问根节点的的左子树;访问根节点;访问根节点的右子树。
二叉树
二叉树是一棵树,其中每个节点都不能有多余两个儿子。
class BinaryNode{
Object element;
BinaryNode left;
BinaryNode right;
}
具有N个节点的每一棵二叉树都将需要N+1个null链。(2N(总边树) – (N – 1)(树的边数))
表达式树
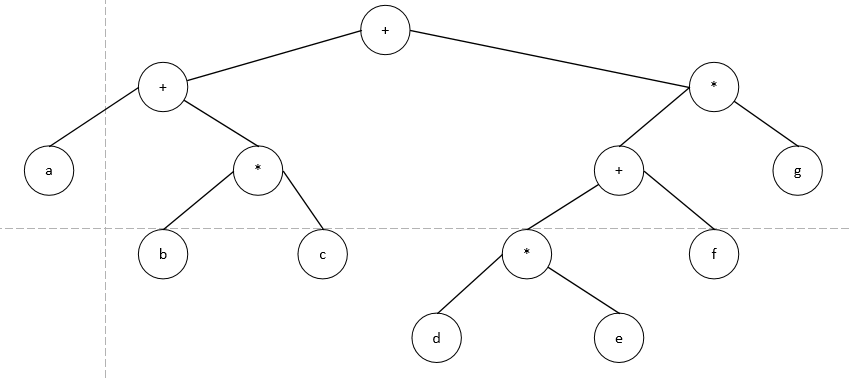
表达式树:树叶是操作数(常数或者是变量名),而其他节点为操作符。
对表达式树进行中序遍历就能到了中缀表达式,后序遍历则是后缀表达式。
上图为(a+b*c)+((d*e+f)*g)的表达式树。
构造表达式树
对于一个后缀表达式。如果符号的操作数,则建立一个单节点并将它推入栈中,如果符号的操作数,那么就从栈中弹出两棵树T1和T2(先弹出的为右子树)并形成一棵新的树,该树的根就是操作符。
二叉查找树
使二叉树成为二叉查找树的性质是,对于树中的每个节点X,它的左子树中所有的项的值都小于X,它的右子树中所有项的值都大于X。二叉查找树的平均深度为O(logN)
代码实现:
public class BinarySearchTree<T extends Comparable<? super T>> {
private static class BinaryNode<T> {
T element;
BinaryNode<T> left;
BinaryNode<T> right;
BinaryNode(T e) {
this(e, null, null);
}
BinaryNode(T e, BinaryNode<T> l, BinaryNode<T> r) {
element = e;
left = l;
right = r;
}
}
private boolean contains(T x, BinaryNode<T> root) {
if (root == null)
return false;
int compare = x.compareTo(root.element);
if (compare > 0)
return contains(x, root.right);
else if (compare < 0)
return contains(x, root.left);
else
return true;
}
private BinaryNode<T> findMax(BinaryNode<T> root) {
if (root == null)
return null;
else if (root.right == null)
return root;
return findMax(root.right);
}
private BinaryNode<T> findMin(BinaryNode<T> root) {
if (root == null)
return null;
while (root.left != null)
root = root.right;
return root;
}
private BinaryNode<T> insert(T x, BinaryNode<T> root) {
if (root == null)
return new BinaryNode<T>(x);
int compare = x.compareTo(root.element);
if (compare > 0)
root.right = insert(x, root.right);
else if (compare < 0)
root.left = insert(x, root.left);
return root;
}
private BinaryNode<T> remove(T x, BinaryNode<T> root) {
if (root == null)
return root;
int compare = x.compareTo(root.element);
if (compare > 0)
root.right = remove(x, root.right);
else if (compare < 0)
root.left = remove(x, root.left);
//左右子树都不为空,则将待删除的节点的值设为右子树中最小的(不会有左儿子,会方便第二次remove),再从右子树中删除改值。
else if (root.left != null && root.right != null){
root.element = findMin(root.right).element;
root.right = remove(root.element, root.right);
}else//涵盖了一个为空或者两个都为空的情况
root = (root.left != null) ? root.left : root.right;
return root;
}
}
AVL树
REF:http://blog.csdn.net/pacosonswjtu/article/details/50522677
一个AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。
插入一个节点可能破坏AVL树的特性,而这总可以通过对树进行简单的修正来做到,我们称其为旋转。
单旋转:插入点不介于不满足AVL条件的树根和树根对应孩子节点之间
双旋转:插入点介于不满足AVL条件的树根和树根对应孩子节点之间
旋转轴:插入点的直接父节点
不满足AVL条件的树根:深度最深的那个不满足AVL条件的节点
伸展树
伸展树的想法是,当一个节点被访问后,它就要经过一系列的AVL树的旋转被推到根上。
B+树
大O分析假设所有的操作耗时都是相等的,但是当涉及到磁盘I/O的时候,对于磁盘的访问就非常耗时,因此为了节省磁盘访问,我们愿意进行大量的计算。
B+树:是应文件系统所需而产生的一种B-tree的变形树(多叉树)。内部节点不保存信息,叶子节点保存一个磁盘区域。
为什么说B+树比B树更适合实际应用中操作系统的文件索引和数据库索引?
- B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
- B+树的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
数据库索引采用B+树的主要原因是 B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题,B+树应运而生。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作(或者说效率太低)。
Java中的HashMap
Hash table based implementation of the Map interface. This implementation provides all of the optional map operations, and permits null values and the null key. (The HashMap class is roughly equivalent to Hashtable, except that it is unsynchronized and permits nulls.) This class makes no guarantees as to the order of the map; in particular, it does not guarantee that the order will remain constant over time.
Initial capacity: The capacity is the number of buckets in the hash table, The initial capacity is simply the capacity at the time the hash table is created.
Load factor: The load factor is a measure of how full the hash table is allowed to get before its capacity is automatically increased.
HashMap内部是通过哈希表来存储的,所谓哈希表其实就是数组+链表。通过哈希值来计算数组下标,再通过链表的形式将Entry存在相应的数组位置。
HashMap内部数据结构
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
HashMap的put方法
public V put(K key, V value) {
//计算的是key的hash值
return putVal(hash(key), key, value, false, true);
}
/**
* Implements Map.put and related methods
*
* @param hash hash for key
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//table即为存储数据的哈希表
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//如果数组对应索引的值为null,则直接插入
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
//如果key一样,可以看到equals()的作用是用来判断key是否冲突
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
//如果是红黑树
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
//如果是链表
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
//判断是否需要转成红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
//写入
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
//扩容
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
HashMap的get方法
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
/**
* Implements Map.get and related methods
*
* @param hash hash for key
* @param key the key
* @return the node, or null if none
*/
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
//在红黑树中找
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
//在链表中找
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
HashMap的hash函数
/**
* Computes key.hashCode() and spreads (XORs) higher bits of hash
* to lower. Because the table uses power-of-two masking, sets of
* hashes that vary only in bits above the current mask will
* always collide. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward. There is a tradeoff between speed, utility, and
* quality of bit-spreading. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading), and because we use trees to handle large sets of
* collisions in bins, we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage, as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds.
*/
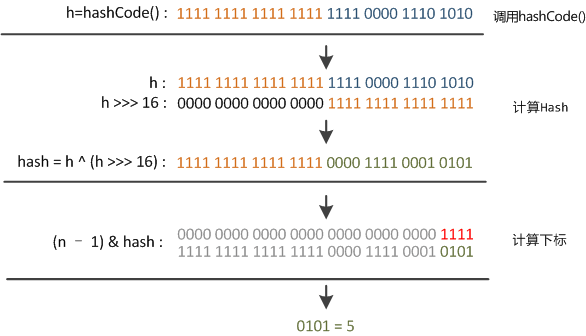
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
算下标的时候是通过(n – 1) & hash来算的,如果n比较小,例如15(0x1111)那么真正起效的只有低4位的值,容易碰撞。因此设计者使用了高16和低16异或了一下。
HashMap的resize方法
/**
* Initializes or doubles table size. If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
//threshold: The next size value at which to resize (capacity * load factor).
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
//超过最大值则不扩充
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
// 把每个bucket都移动到新的buckets中
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}



相关文章